Outils d'utilisateurs
Ceci est une ancienne révision du document !
−Table des matières
Les nombres entiers
Dans les chapitres précédents, vous avez appris à utiliser std::cout pour afficher des messages. Les messages sont des chaînes de caractères encadrées par des guillemets droits ”. Une valeur écrite directement dans le code C++ est appelée une littérale. Il existe d'autres types de littérales, par exemple :
- les nombres entiers :
0,1,2,-1,-2; - les nombres réels :
1.0,2.1,-5.12,1.457; - les booléens, qui représente une valeur à deux états :
true(vrai) etfalse(faux) ; - les caractères : 'a', 'b', 'c' ;
- les chaînes de caractères (que vous avez déjà vu) : “hello, world”, “salut tout le monde”.
Remarquez bien la différence entre les caractères, qui s'écrivent avec des guillemets droits simples, et les chaînes, qui s'écrivent avec des guillemets droits doubles. Notez aussi que les nombres réels s'écrivent avec un point (notation anglaise) et non avec une virgule (notation française).
Vous pouvez afficher ces littérales directement en utilisant std::cout, comme vous l'avez vu pour les chaînes de caractères.
- main.cpp
#include <iostream> int main() { std::cout << 1 << std::endl; // nombre entier std::cout << 3.1415 << std::endl; // nombre réel std::cout << true << std::endl; // booléens std::cout << 'a' << std::endl; // caractère std::cout << "hello, world!" << std::endl; // chaîne de caractères }
Nous reviendrons par la suite les spécificités de chaque type de littérales, voyons pour le moment les nombres entiers plus en détail.
Écrire des nombres entiers
Les nombres entiers ne devraient pas vous poser de problème, ce sont les nombres que vous utiliser pour compter depuis l'école maternelle. La forme la plus simple pour écrire un nombre entier est d'écrire une série continue de chiffres entre 0 et 9.
- main.cpp
#include <iostream> int main() { std::cout << 1 << std::endl; // affiche le nombre 1 std::cout << 2 << std::endl; // affiche le nombre 2 std::cout << 3 << std::endl; // affiche le nombre 3 std::cout << 4 << std::endl; // affiche le nombre 4 }
Pour écrire un nombre entier négatif, vous devez ajouter le signe moins devant le nombre.
- main.cpp
#include <iostream> int main() { std::cout << -1 << std::endl; // affiche le nombre -1 std::cout << -2 << std::endl; // affiche le nombre -2 std::cout << -3 << std::endl; // affiche le nombre -3 std::cout << -4 << std::endl; // affiche le nombre -4 }
Lorsque vous écrivez de très grands nombres, il peut être difficile de les lire. Par exemple :
- main.cpp
#include <iostream> int main() { std::cout << 123456789123456789 << std::endl; }
La raison est que le cerveau humain est capable de reconnaître des groupes de quelques caractères, mais pas un seul bloc de 18 caractères. Il n'arrive donc pas, en un coup d’œil, à identifier si ce nombre est de l'ordre du million, du milliard ou autre.
Pour faciliter la lecture, il est possible d'ajouter un caractère guillemet droit simple ' pour séparer un grand nombre en plusieurs groupes. Par habitude, on sépare en groupes de trois chiffres :
- main.cpp
#include <iostream> int main() { std::cout << 123'456'789'123'456'789 << std::endl; }
Notez bien que la différence entre le guillemet droit simple utilisé pour écrire une littérale de type caractère et le séparateur numérique. Si la littérale commence par un un guillemet, elle sera considérée comme étant un caractère.
- main.cpp
#include <iostream> int main() { std::cout << 4'56 << std::endl; // ok, séparateur numérique std::cout << '456 << std::endl; // erreur, guillemet manquant (1) std::cout << '456' << std::endl; // erreur, plusieurs caractères (2) }
La première erreur se produit du fait que le compilateur pense que le guillemet correspond au début d'une littérale caractère, mais ne trouve pas la fin.
main.cpp:5:18: warning: missing terminating ' character [-Winvalid-pp-token]
std::cout << '456 << std::endl;
^
La seconde erreur correspond à une littérale caractère qui contient plusieurs caractères.
main.cpp:6:18: warning: multi-character character constant [-Wmultichar]
std::cout << '456' << std::endl;
^
Vous pouvez écrire des nombres très grand de cette manière, mais il existe une limite. Si vous écrivez un nombre trop grand, vous aurez un message d'erreur signalant que ce nombre est trop grand.
- main.cpp
#include <iostream> int main() { std::cout << 123456789123456789123456789123456789 << std::endl; }
produira l'erreur :
main.cpp:4:18: error: integer literal is too large to be represented in any integer type
std::cout << 123456789123456789123456789123456789 << std::endl;
^
L’existence d'une valeur maximale limite est liée à la représentation des nombres dans la mémoire des ordinateurs et à la notion de type de données. Vous verrez cela dans les prochains chapitres.
Les nombres décimaux, hexadécimaux, octaux et binaires
Les nombres entiers que vous utilisez habituellement s'écrivent à partir de dix chiffres (0 à 9). C'est pour cette raison que l'on parle de système décimal (du latin decimus, qui signifie “dixième”) et de base 10. Mais ce n'est pas la seule façon d'écrire les nombres et il existe d'autres systèmes numériques.
Imaginons par exemple que vous souhaitez écrire des nombres en utilisant que huit chiffres (0 à 7 - base 8). Dans ce cas, nous pouvons compter de la façon suivante : 0, 1, 2, 3, 4, 5, 6, 7. Arrivé au huitième chiffre, nous ne pouvons pas écrire “8”, puisque ce chiffre n'est pas autorisé dans ce système. Donc, il faut passer à un nombre à deux chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, etc.
En C++, il est possible d'écrire et afficher des nombres écrits selon des bases différentes de 10. Pour des raisons historiques et matériel, les ordinateurs savent manipuler les nombres en base 2 (binaire), 8 (octal), 10 (décimal) et 16 (hexadécimal). Pour écrire un nombre dans une base différente de 10, il faut commencer le nombre par le chiffre 0 puis un caractère optionnel pour spécifier la base : rien pour octal, x ou X pour l'hexadécimal et b pour le binaire. Les chiffres autorisés pour écrire un nombre dépendent de la base utilisée : 0 à 7 pour l'octal, 0 à 9 et a à f (ou A à F) pour l'hexadécimal et 0 et 1 pour le binaire.
Le code suivant permet d'afficher la valeur de 10 selon la base :
- main.cpp
#include <iostream> int main() { std::cout << 10 << std::endl; std::cout << 010 << std::endl; std::cout << 0x10 << std::endl; std::cout << 0b10 << std::endl; }
affiche :
10 8 16 2
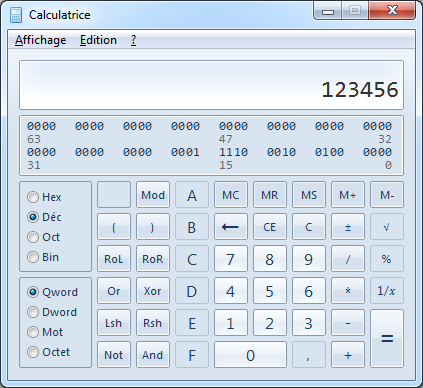
Il est possible réaliser ces conversions à la main, mais c'est plus simple d'utiliser un logiciel de conversion. Il existe des convertisseurs en ligne, vous pouvez également utiliser la calculatrice de Windows en sélectionnant le mode “Programmeur” dans le menu “Affichage”.
Il faut donc bien faire attention à la base utilisée lorsque l'on écrit un nombre.
| Base | Système | Préfixe | Chiffres | Exemple |
|---|---|---|---|---|
| 2 | binaire | 0b | 0 et 1 | 0b01 |
| 8 | octal | 0 | 0 à 7 | 001234567 |
| 10 | décimal | 0 à 9 | 1234567890 |
|
| 16 | hexadécimal | 0x | 0 à 9 et a à f | 0x0123456789abcdef |
| 0X | 0 à 9 et A à F | 0X0123456789ABCDEF |
Comme vous l'avez vu dans les codes précédents, les nombres sont affichés après conversion en base 10. C'est le mode de fonctionnement par défaut de std::cout, mais il est possible de modifier ce comportement. Les directives (I/O manipulator) suivantes permettent de modifier la base utilisée par std::cout pour afficher les nombres :
std::octpour afficher en utilisant la base 8 ;std::decpour afficher en utilisant la base 10 ;std::hexpour afficher en utilisant la base 16.
Il n'existe pas de directive permettant d'afficher les nombres en binaire. Vous pourrez réaliser cela dans un exercice, dans la suite du cours.
- main.cpp
#include <iostream> int main() { std::cout << std::hex; std::cout << 10 << std::endl; std::cout << 010 << std::endl; std::cout << 0x10 << std::endl; std::cout << 0b10 << std::endl; }
affiche :
a 8 10 2
Comme vous le voyez, une directive continue de s'appliquer sur toutes les lignes suivantes, tant que vous ne donner pas une directive modifiant une nouvelle fois l'affichage. Vous pouvez écrire les directives sur une ligne différente (comme dans le code précédent), sur la première ligne ou à chaque ligne, cela ne change rien au résultat.
std::endl, qui ont un effet immédiat, et les directives comme std::hex, qui ont un effet permanent, jusqu'à ce qu'une autre directive modifie le comportement.
Si vous affichez des nombres en utilisant plusieurs bases différentes, il peut être difficile de savoir à quelle base correspond chaque nombre affiché. Il est possible d'afficher la base utilisée pour l'affichage avec la directive std::showbase. Pour ne plus afficher la base, vous pouvez utiliser la directive std::noshowbase.
- main.cpp
#include <iostream> int main() { std::cout << 10 << std::endl; std::cout << 010 << std::endl; std::cout << 0x10 << std::endl; std::cout << 0b10 << std::endl; std::cout << std::endl; std::cout << std::hex << std::showbase; std::cout << 10 << std::endl; std::cout << 010 << std::endl; std::cout << 0x10 << std::endl; std::cout << 0b10 << std::endl; }
affiche :
10 8 16 2 0xa 0x8 0x10 0x2
Les opérations arithmétiques sur les entiers
Pouvoir écrire et afficher des nombres entiers est un début, mais il est possible d'aller plus loin et de réaliser des calculs dessus. Pour cela, le C++ propose plusieurs opérateurs naturels de l'arithmétique, comme l'addition +, la soustraction - ou la multiplication *.
- main.cpp
#include <iostream> int main() { std::cout << "123 + 456 = " << 123 + 456 << std::endl; std::cout << "123 - 456 = " << 123 - 456 << std::endl; std::cout << "123 * 456 = " << 123 * 456 << std::endl; }
affiche :
123 + 456 = 579 123 - 456 = -333 123 * 456 = 56088
Il est également possible de calculer des divisions entières avec l'opérateur division / et de calculer le reste d'une division entière avec l'opérateur modulo %. Pour rappel, la division entière permet de calculer le résultat d'une division en utilisant uniquement des nombres entiers (c'est le premier type de division que vous avez appris à l'école). Ainsi :
- avec une division entière : 11 divisé par 4 donne 2 et reste 3 ;
- avec une division réelle : 11 divisé par 4 donne 2,75.
- main.cpp
#include <iostream> int main() { std::cout << "10 / 2 = " << 10 / 2 << std::endl; std::cout << "10 / 3 = " << 10 / 3 << std::endl; std::cout << "10 / 4 = " << 10 / 4 << std::endl; std::cout << "10 % 2 = " << 10 % 2 << std::endl; std::cout << "10 % 3 = " << 10 % 3 << std::endl; std::cout << "10 % 4 = " << 10 % 4 << std::endl; }
affiche :
10 / 2 = 5 10 / 3 = 3 10 / 4 = 2 10 % 2 = 0 10 % 3 = 1 10 % 4 = 2
/ est utilisé pour faire les divisions entières et réelles. Il faut donc particulièrement faire attention de ne pas se tromper lorsque l'on écrit une expression, sous peine d'avoir des résultats étranges.
- main.cpp
#include <iostream> int main() { std::cout << "11 / 4 = " << 11 / 4 << std::endl; // division entière std::cout << "11.0 / 4.0 = " << 11.0 / 4.0 << std::endl; // division réelle }
affiche :
11 / 4 = 2 11.0 / 4.0 = 2.75
Les opérations mathématiques suivent la sémantique habituelle, en particulier pour l'ordre d'évaluation et l'utilisation des parenthèses. Pour rappel, pour évaluer une expression mathématique (une série de plusieurs opérations), l'ordre d'évaluation est le suivant :
- en premier, évaluer les expressions entre parenthèse ;
- ensuite, évaluer les multiplications et les divisions ;
- pour terminer, évaluer les additions et les soustractions.
Ainsi, l'expression ci-dessous s'évalue de la façon suivante :
5 - (2 + 3) / 4 = 5 - 5 / 4 = 5 - 1 = 4
Pour exercice, écrivez le code C++ correspondant pour évaluer cette expression et vérifier que le résultat est correct.
De la même façon, les opérateurs du C++ suivent les règles arithmétiques habituelles :
- la commutativité (sauf pour la division) : a + b = b + a ;
- l'associativité : a + (b + c) = (a + b) + c ;
- la distributivité : a * (b + c) = a * b + a * c.
On peut vérifier facilement ces règles avec un programme C++ :
- main.cpp
#include <iostream> int main() { std::cout << "Commutativité :" << std::endl; std::cout << "2 + 3 = " << 2 + 3 << std::endl; std::cout << "3 + 2 = " << 3 + 2 << std::endl; std::cout << "Associativité :" << std::endl; std::cout << "2 + (3 + 4) = " << 2 + (3 + 4) << std::endl; std::cout << "(2 + 3) + 4 = " << (2 + 3) + 4 << std::endl; std::cout << "Distributivité :" << std::endl; std::cout << "2 * (4 + 3) = " << 2 * (4 + 3) << std::endl; std::cout << "2 * 4 + 2 * 3 = " << 2 * 4 + 2 * 3 << std::endl; }
affiche :
Commutativité : 2 + 3 = 5 3 + 2 = 5 Associativité : 2 + (3 + 4) = 9 (2 + 3) + 4 = 9 Distributivité : 2 * (4 + 3) = 14 2 * 4 + 2 * 3 = 14
Les comportements indéfinis
Un dernier point pour terminer, essayez de diviser un nombre entier par zéro :
- main.cpp
#include <iostream> int main() { std::cout << "1 / 0 = " << (1 / 0) << std::endl; }
Ce code affichera un avertissement (warning) à la compilation, vous informant que la division par zéro n'est pas définie :
main.cpp:4:20: warning: division by zero is undefined [-Wdivision-by-zero]
std::cout << (1/0) << std::endl;
^~
On parle en C++ de “comportement indéfini”, undefined behavior en anglais, que l'on abrège parfois avec les initiales “UB”. Cela signifie qu'un programme utilisant un tel code aura un comportement aléatoire et pourra faire n'importe quoi : provoquer une erreur, donner un résultat quelconque ou encore sembler fonctionner correctement. Les comportements indéfinis sont difficile à corriger, puisque cela ne produit pas forcement un message d'erreur clair.
Ainsi, l'exécution du programme précédent se déroule sans erreur à l'exécution. Par contre, la valeur affichée par std::cout est aléatoire (dans Coliru.com) et n'a pas de sens en termes mathématiques :
1 / 0 = 4196864
Le C++ étant un langage permissif, le compilateur ne va pas nécessairement vérifier que vous écrivez du code incorrect. C'est de votre responsabilité de vérifier que le code ne provoque pas de comportement indéfini. Pour cela, voici quelques aides :
Respectez les bonnes pratiques de codage. Comme le C++ est permissif, le développeur a le droit d'écrire du code correct ou du code incorrect. Cela peut paraître évident, mais il vaut mieux le dire : il est préférable d'écrire du code correct que du code incorrect ! Il y a souvent plusieurs façons en C++ de résoudre un même problème, certaines approches posent davantage de problèmes que d'autres.
Ce cours de C++ n'a pas pour vocation à vous apprendre tout le C++. Il se focalise, volontairement, sur les syntaxes les plus récentes et les plus sûres. Et même en utilisant ces approches modernes, il y aura des précautions à prendre pour éviter les problèmes. Vous apprendrez à écrire du code le plus sécurisé possible.
Faites vous aider par le compilateur. Celui-ci peut faire certaine vérifications, comme dans le code précédent, et vous avertir lorsque vous écrivez un code qui pose potentiellement un problème. Tous les compilateurs ne font pas les mêmes vérifications et les contrôles effectués dépendent des options utilisées. Les options -Wall -Wextra -pedantic qui vous ont été présenté dans coliru.com activent les principales vérifications, mais il en existe d'autres. Il peut être intéressant de compiler un code avec plusieurs compilateurs pour avoir un maximum de messages d'avertissement.
Utilisez les outils de vérifications statique et dynamique. Ce sont des outils qui font plus de vérifications que le compilateur. Les premiers vérifient le code directement, alors que les secondes travaillent sur le programme après compilation (donc durant l'exécution).
Non seulement ils permettent de vérifier le respect des règles du langage C++, mais également que certaines pratiques de codage sont respectées. Dans l'objectif d'écrire des programmes C++ modernes, il ne faut pas hésiter à utiliser ce type d'outils. Vous verrez dans la suite de ce cours comment installer et utiliser certains de ces outils.
Exercices
cf http://openclassrooms.com/forum/sujet/exercices-dans-le-cours-de-gbdivers
Remarque : le but de ces exercices est de faire des calculs arithmétiques de base. C'est assez simple, ce n'est pas vraiment de la programmation (c'est surtout pour jouer avec l'affichage et les opérations de base). Mais c'est quelque chose que l'on doit savoir faire (même à la main, avec crayon et papier)
Conversion en nombre de n'importe quelle base
http://fr.wikipedia.org/wiki/Syst%C3%A8me_d%C3%A9cimal
opérations à faire pour les calculs ?
Le but de cet exercice est de convertir un nombre d'une base donnée en une autre base. (comme c'est le début du cours, il ne faudra utiliser que les opérations mathématiques et l'affichage, donc pas de boucles et fonctions). Par exemple convertir 1234 en hexadécimal ou 0xabc en décimal. (le but est de pratiquer les conversions de bases, pas d'écrire un code de conversion réutilisable). Tu peux prendre n'importe quel nombre dans n'importe quelle base (en utilisant les préfixes), l'afficher dans une autre base (en utilisant std::hex, std::dec, etc), puis ecrire un code qui affiche la conversion, mais faite manuellement.
Calculer l'indice de colonne et de ligne d'une table
Cet exercice consiste à calculer la ligne et la colonne correspondant à un index donné (c'est très utile pour les tableaux à plusieurs dimensions). Pour cet exo, imaginez un tableau suivant :
0 1 2 3 4 5 6 7 8 9 10 11
(on appelle ce tableau “row major” puisque les données sont en ligne en premier, cf http://en.wikipedia.org/wiki/Row-major_order). Si on donne un élément du tableau (par exemple 6), il faut trouver le numéro de ligne et le numéro de colonne correspondant, en utilisant les opérateurs / et %. Faire de même avec d'autres tableaux (dont des tableaux en column major). Remarque : en C++, on compte à partir de 0. Donc les colonnes et lignes s'écrivent 0, 1, 2, … (et pas 1, 2, 3, …)
Préliminaire : Je veux l'indice du tableau 1D qui correspond à la case (x,y) de mon tableau 2D, sachant que j'ai rangé mes lignes l'une derrière l'autre, d'abord la première ligne, ensuite la seconde …
Pour la découvrir empiriquement, quelle est l'indice de la première colonne de la première ligne? Quel est l'indice de la dernière colonne de la première ligne? Quel est l'indice de la première colonne de la seconde ligne? quelle est l'indice de la dernière colonne de la seconde ligne?, quel est l'indice de la dernière colonne de la dernière ligne?, Quel est l'indice de la première colonne de la dernière ligne? et pour finir quel est l'indice d'une case (x,y) quelconque du tableau 2D?
Sachant qu'a chaque indice du tableau 1D il y a une seule position (x,y) qui correspond, et que chaque position (x,y) correspond un seul indice du tableau 1D, si tu connais la formule dans un sens, découvrir la formule dans l'autre sens ne sera pas très difficile ;).
A partir d'un élément du tableau (par exemple i = 6, i pour index), tu as besoin de connaitre la largeur (w = 4, w pour width) et la hauteur (h = 3, h pour height) du tableau et d'utiliser les opérateurs division entière / et modulo %. Tu dois obtenir pour i = 6, x = 2 (numéro de colonne) et y = 1 (numéro de ligne).
Si ta formule est bonne, cela veut dire qu'en appliquant la même formule sur un autre indice du tableau ou un autre tableau, le numéro de ligne et de colonne devraient être bons. Est-ce que c'est le cas ? Essaie par exemple, avec le même tableau, avec l'indice 7 par exemple (cela doit donner ligne=1 et colonne=3)
Remarque : Une division entière (comme on l'apprend en primaire : image) peut s’écrire :
dividende = diviseur * quotient + reste
La division entière et le modulo sont les opérations qui permettent d'avoir le quotient et le reste :
division(dividande, diviseur) = quotient modulo(dividande, diviseur) = reste
En C++, on va écrire :
const auto quotient = dividende / diviseur; const auto reste = dividende % diviseur;
Des compteurs finis
Un autre exercice avec modulo : imaginons que l'on a un compteur qui compte jusqu'à 100. Comment transformer ce compteur en compteur qui compte de 0 à 10 en boucle ? (ie, dois retourner 0, 1, …, 8, 9, 0, 1, …)
Faire de même pour compter de 3 à 8 en boucle.