Outils d'utilisateurs
Table des matières
Logique binaire et calcul booléen
La représentation en base 2, le binaire, possède une importance particulière en informatique. Vous avez vu dans les chapitres précédents que vous pouvez représenter les nombres entiers sous forme binaire (une suite de 0 et de 1) en utilisant le préfixe 0b. Vous pouvez également écrire des valeurs booléennes en utilisant les mots-clés true (vrai) et false (faux).
Cette forme de logique est tellement importante qu'un chapitre complet lui est consacré (et vous reviendrez plusieurs fois sur ces notions durant le cours).
En électronique, il est facile de représenter des valeurs binaires en utilisant des tensions différentes. Par exemple, on va définir que l'état “vrai” sera représenté par une tension de +5V et l'état “faux” par une tension de 0V. (En pratique, les valeurs prises seront très variables selon les composants de l'ordinateur, mais le principe reste le même.)
Ces valeurs binaires utilisées en interne sont appelées “bits” et correspondent au plus petit élément d'information que peut manipuler un ordinateur. Tous les autres types de données (aussi bien les nombres que les chaînes de caractères) sont définis à partir d'une représentation interne en bits. Même les nombres binaires et les booléens que vous utilisez en C++ sont représentés par des bits dans l'ordinateur.
Il est possible en C++ de manipuler directement les représentations internes des valeurs, mais cela est beaucoup plus complexe et moins sécurisé que de manipuler les types du C++. Vous n'aurez besoin de faire cela que dans des cas très spécifiques (programmation de micro-contrôleur, optimisation bas niveau), mais vous verrez comment faire cela.
La notation des valeurs binaires “vrai” et “faux” est purement arbitraire. Vous pouvez définir que les valeurs binaires sont “haut” et “bas”, “droite” et “gauche” ou n'importe quoi d'autre. Le plus important est que cela représente deux états différents. Dans du code C++, vous avez deux manières de représenter les valeurs binaires :
- avec 0 et 1, pour représenter un nombre entier ;
- avec
falseettrue, pour représenter un booléen.
Les booléens
Voyons dans un premier temps les valeurs binaires, encore appelées booléens (nom donné en l'honneur du mathématicien George Boole, qui a créé cette branche des mathématiques).
Afficher une valeur booléenne
Pour écrire une valeur booléenne, il faut utiliser les mots-clé true (vrai) et false (faux). Par défaut, std::cout affiche ces valeurs avec respectivement 1 et 0. La directive std::boolalpha permet d'afficher les booléens en clair et la directive std::noboolalpha permet d'arrêter de représenter les booléens.
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "false = " << false << std::endl; std::cout << "true = " << true << std::endl; std::cout << std::noboolalpha; std::cout << "false = " << false << std::endl; std::cout << "true = " << true << std::endl; }
affiche :
false = false true = true false = 0 true = 1
Les opérateurs logiques
Les booléens ne se manipulent pas comme des nombres entiers. En effet, cela n'a pas de sens de faire des opérations arithmétiques dessus. Les booléens permettent un nombre limité d'opérations logiques, qui prennent un ou deux booléens et retournent un nouveau booléen.
true + 2. La raison est que les valeurs booléennes sont représentées en interne par des nombres (généralement 0 et 1) et que cela a un sens, pour l'ordinateur, de faire ce type d'opération.
Mais cela n'a pas de sens en termes de logique (quel sens pourrait-on donner à l'expression true + 2 ?).
En C++, on utilisera les mots-clés true et false. Le respect des types est l'une des forces du C++, encore faut-il les utiliser correctement. Le C++ est un langage permissif, il autorisera à écrire true + 2, mais cela brisera la sémantique des booléens.
La première opération booléenne est la négation “NON” !, qui transforme true en false et false en true :
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "!false = " << !false << std::endl; std::cout << "!true = " << !true << std::endl; }
affiche :
!false = true !true = false
La seconde opération est la conjonction &&, qui prend deux booléens et retourne vrai uniquement si les deux booléens valent vrai. Cette opération est également appelée “AND” ou “ET”, puisque pour que le résultat soit vrai, il faut que le premier booléen soit vrai ET que le second booléen soit vrai.
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "false AND false = " << (false && false) << std::endl; std::cout << "false AND true = " << (false && true) << std::endl; std::cout << "true AND false = " << (true && false) << std::endl; std::cout << "true AND true = " << (true && true) << std::endl; }
affiche :
false AND false = false false AND true = false true AND false = false true AND true = true
La dernière opération est la disjonction ||, qui prend également deux booléens et retourne vrai si au moins un des deux booléens est vrai. Cette opération est également appelée “OR” ou “OU”, puisque pour que le résultat soit vrai, il faut que le premier booléen soit vrai OU que le second booléen soit vrai.
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "false OR false = " << (false || false) << std::endl; std::cout << "false OR true = " << (false || true) << std::endl; std::cout << "true OR false = " << (true || false) << std::endl; std::cout << "true OR true = " << (true || true) << std::endl; }
affiche :
false OR false = false false OR true = true true OR false = true true OR true = true
|| retourne vrai si les deux opérandes sont vraies, on dit que c'est un “OU inclusif”. Il faut donc comprendre le “OU” de la façon suivante : “le premier booléen est vrai OU le second booléen est vrai OU les deux sont vrais”.
La seconde version de la disjonction est le “OU exclusif” ou “XOR”. Dans ce cas, il faut prendre le “OU” au sens strict : “le premier booléen est vrai OU le second booléen est vrai, mais pas les deux en même temps”.
Il n'existe pas en C++ d'opérateur logique “Ou exclusif”, mais il est possible de le simuler avec les autres opérateurs.
Ces opérateurs peuvent être résumés dans un tableau (appelé table de vérité) :
a | b | !a | a && b | a || b |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
Pour terminer, les opérateurs logiques du C++ fonctionnent en utilisant l'évaluation paresseuse (lazy evaluation). Cela permet d'évaluer les opérandes uniquement si nécessaire. Imaginons les opérations suivantes, dans lesquelles “expression complexe” est un code quelconque qui prend du temps pour être évalué :
a && (expression complexe) b || (expression complexe)
Avec le tableau précédent, on peut remarquer que si a est faux, alors le résultat de a && (expression complexe) sera toujours faux, quelle que soit la valeur de expression complexe. Dans ce cas, il n'est pas nécessaire d'évaluer “expression complexe”, puisque sa valeur ne change pas le résultat.
De la même façon, si b est vrai dans la seconde expression, le résultat de b || (expression complexe) sera toujours vrai quelle que soit la valeur de expression complexe, il n'est pas nécessaire d'évaluer expression complexe.
Les opérateurs de comparaison
Généralement, vous n'aurez pas à écrire true et false directement dans vos codes, vous manipulerez des booléens générés par des tests. Un test est simplement une expression (une suite d'instructions et de calculs) qui retourne un booléen. Les opérateurs logiques permettent de combiner des tests simples pour former des tests plus complexes, voire très complexes.
Une méthode classique pour écrire une expression retournant un booléen est d'utiliser les opérateurs de comparaison. Comme leur nom l'indique, ces opérateurs permettent de comparer des valeurs et de retourner vrai ou faux, selon le résultat de cette comparaison. Ces opérateurs sont les suivants :
- l'opérateur “EST ÉGAL À”
==permet de tester si deux valeurs sont égales ; - l'opérateur “EST DIFFÉRENT DE”
!=permet de tester si deux valeurs sont différentes ; - l'opérateur “EST SUPÉRIEUR À”
>permet de tester si la première valeur est supérieure à la seconde ; - l'opérateur “EST SUPÉRIEUR OU ÉGAL À”
>=permet de tester si la première valeur est supérieure ou est égale à la seconde ; - l'opérateur “EST INFÉRIEUR À”
<permet de tester si la première valeur est inférieure à la seconde ; - l'opérateur “EST INFÉRIEUR OU ÉGAL À”
⇐permet de tester si la première valeur est inférieure ou est égale à la seconde.
Ces opérateurs peuvent s'appliquer sur des nombres entiers, des réels ou des caractères, par exemple :
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "12.34 == 23.45 ? " << (12.34 == 23.45) << std::endl; std::cout << "12.34 != 23.45 ? " << (12.34 != 23.45) << std::endl; std::cout << "12.34 > 23.45 ? " << (12.34 > 23.45) << std::endl; std::cout << "12.34 >= 23.45 ? " << (12.34 >= 23.45) << std::endl; std::cout << "12.34 < 23.45 ? " << (12.34 < 23.45) << std::endl; std::cout << "12.34 <= 23.45 ? " << (12.34 <= 23.45) << std::endl; }
affiche :
12.34 == 23.45 ? false 12.34 != 23.45 ? true 12.34 > 23.45 ? false 12.34 >= 23.45 ? false 12.34 < 23.45 ? true 12.34 <= 23.45 ? true
Pour les nombres, ces opérateurs ne posent pas de difficultés particulières, leur fonctionnement correspond à ce que vous connaissez en mathématique.
Comme le langage C++ est permissif, la comparaison de valeurs de types différents ne produira pas forcément une erreur de compilation. Par exemple comparer un entier et un caractère :
#include <iostream> int main() { std::cout << std::boolalpha << ('a' < 42) << std::endl; }
Par contre, cela n'a pas de sens en termes de sémantique (comme on dit, on ne compte pas ensembles des pommes et des poires), il ne faut donc pas écrire ce type de code. En revanche, vous pouvez combiner le résultat de plusieurs comparaisons sur des valeurs de types différents en utilisant les opérateurs logiques :
#include <iostream> int main() { std::cout << std::boolalpha << (('a' < 'z') && (123 >= 456)) << std::endl; }
Exercices
- Evaluer le résultat de ces expressions (à la main, pas avec du code) :
a | b | !a && b | !a || b | !a && !b | !a || !b |
|---|---|---|---|---|---|
| 0 | 0 | ? | ? | ? | ? |
| 0 | 1 | ? | ? | ? | ? |
| 1 | 0 | ? | ? | ? | ? |
| 1 | 1 | ? | ? | ? | ? |
- Un OU Exclusif correspond à la table de vérité suivante.
a | b | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Dans le code suivant, replacer @@@@ par une expression n'utilisant que les valeurs a et b et les opérateurs logiques &&, || et !, de façon à reproduire la table de vérité précédente.
- main.cpp
#include <iostream> bool eval(bool a,bool b) { return (@@@@); } int main() { std::cout << std::noboolalpha; std::cout << "| a | b | XOR " << std::endl; std::cout << "| 0 | 0 | " << eval(false, false) << std::endl; std::cout << "| 0 | 1 | " << eval(false, true) << std::endl; std::cout << "| 1 | 0 | " << eval(true, false) << std::endl; std::cout << "| 1 | 1 | " << eval(true, true) << std::endl; }
Représentation binaire des entiers
Comme vous l'avez vu dans les chapitres précédents, la façon dont vous écrivez un nombre dans le code et la façon dont il est affiché dans la console sont indépendants. Par défaut, l'écriture d'un nombre et son affichage se font en utilisant la base 10 (décimal), mais vous pouvez changer la base lors de l'écriture en utilisant un préfixe (0b, 0 et 0x) et lors de l'affichage en utilisant une directive (std::oct, std::dec et std::hex).
- main.cpp
#include <iostream> int main() { std::cout << std::showbase << 0b101010 << std::endl; std::cout << std::hex << 0b101010 << std::endl; }
affiche :
42 0x2a
Il n'existe pas de directive pour afficher les nombres directement en binaire, on utilise souvent à la place la représentation hexadécimale. La raison est qu'il est relativement facile de faire la conversion entre hexadécimal et le binaire. En effet, un chiffre hexadécimal correspond exactement à quatre chiffres binaires, il faut donc utiliser la conversion suivante :
| hexadécimal | binaire | hexadécimal | binaire |
|---|---|---|---|
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | a | 1010 |
| 3 | 0011 | b | 1011 |
| 4 | 0100 | c | 1100 |
| 5 | 0101 | d | 1101 |
| 6 | 0110 | e | 1110 |
| 7 | 0111 | f | 1111 |
Ainsi, pour convertir la valeur 0x2a en binaire, vous devez prendre le premier chiffre (2), le convertir en binaire (0010), puis faire la même chose avec le second “chiffre” (a), ce qui donne 1010). La représentation binaire finale est donc 0b00101010.
std::bitset. Cette classe sera étudiée en détail dans un chapitre Complément, mais pour le moment, vous pouvez utiliser la sytnaxe :
- main.cpp
#include <iostream> #include <bitset> int main() { std::cout << "0b" << std::bitset<8>(0b101010) << std::endl; std::cout << "0b" << std::bitset<8>(42) << std::endl; }
affiche :
0b00101010 0b00101010
Le chiffre 8 correspond au nombre de bits à utiliser, pensez à l'adapter si vous utilisez des nombres entiers plus grands. Et n'oubliez pas la directive d'inclusion bitset.
Comme cela a été expliqué au début du chapitre, toutes les valeurs que manipule un ordinateur sont en fait codées en interne en binaire. Cet encodage en binaire dans la mémoire de l'ordinateur est appelée représentation binaire. Vous n'aurez généralement pas besoin de manipuler directement les valeurs sous forme binaire, mais cette représentation est suffisamment importante pour que cela soit détaillé ici.
La conversion des nombres entiers décimaux positifs en binaire est relativement simple. Pour les autres types de données (valeurs entières négatives, nombres réels, chaînes de caractères, etc.), la conversion n'est pas aussi simple et naturelle. Il existe en fait différentes normes de conversion, qui expliquent comment convertir une valeur d'un type donné en sa représentation binaire. Et il existe souvent plusieurs normes pour un même type de données.
Un exemple classique de normalisation d'encodage concerne les caractères. Vous verrez qu'il existe des normes telles que “ASCII”, “Windows-1252” ou “UTF-8”. Au final, il existe des centaines de formes différentes d'encodage.
Heureusement, le compilateur vérifie les types que l'on utilise lorsque l'on fait des conversions, pour que cela conserve un sens. Il faudra juste faire attention de ne pas empêcher le compilateur de faire son travail. Mais nous reviendrons là dessus plus tard.
Une séquence de 8 bits (ou de 2 chiffres hexadécimaux, c'est équivalent) est appelée un octet (1 o), 1024 o donnent 1 kibi-octet (1 Kio), 1024 Kio donnent 1 mébi-octet (1 Mio), 1024 Mio donnent 1 gibi-octet (1 Gio) et 1024 Gio donnent 1 tebi-octet (1 Tio).
Cependant, avec le système métrique, le rapport devrait être de 1000 au lieu de 1024 et certains utilisent volontairement cette différence pour maintenir une ambiguïté chez le lecteur. Voir Préfixe binaire pour plus de détail.
Les opérateurs arithmétiques
Maintenant que vous savez écrire et lire les nombres binaires, vous allez pouvoir les manipuler. Comme ce sont des nombres entiers, les opérateurs arithmétiques présentés dans le chapitre précédent peuvent être utilisés :
- main.cpp
#include <iostream> int main() { std::cout << 0b1010 + 0b1011 << std::endl; // addition std::cout << 0b0011 - 0b1101 << std::endl; // soustraction std::cout << 0b1000 * 0b1011 << std::endl; // multiplication std::cout << 0b1001 / 0b0010 << std::endl; // division entière }
affiche :
21 -10 88 4
Notez bien que ces opérations donnent le même résultat que si vous aviez écrit les nombres en représentation binaire. Par exemple, pour la division :
- main.cpp
#include <iostream> int main() { std::cout << 0b1001 << std::endl; std::cout << 0b0010 << std::endl; std::cout << 9 / 2 << std::endl; std::cout << 0b1001 / 0b0010 << std::endl; }
affiche :
9 2 4 4
Exos : faire une addition et une multiplication binaire “à la main”.
- main.cpp
#include <iostream> #include <bitset> int main() { std::cout << " " << std::bitset<8>(0b0100100) << std::endl; std::cout << "+ " << std::bitset<8>(0b0101001) << std::endl; std::cout << " --------" << std::endl; std::cout << "= " << std::bitset<8>(0b0100100 + 0b0101001) << std::endl; }
affiche :
00100100 + 00101001 -------- = 01001101
L'opérateur négation
En complément de ces opérateurs arithmétiques, il existe des opérateurs travaillant sur la représentation binaire, que l'on appelle opérateurs logiques bit à bit. Le premier opérateur est la négation ~, qui permet d'inverser tous les bits d'un nombre (les 0 deviennent des 1 et les 1 deviennent des 0). Par exemple :
- main.cpp
#include <iostream> #include <bitset> int main() { std::cout << " ~" << std::bitset<8>( 0b0100100) << std::endl; std::cout << "= " << std::bitset<8>(~0b0100100) << std::endl; std::cout << std::endl; std::cout << " ~" << std::bitset<8>( 0b1001011) << std::endl; std::cout << "= " << std::bitset<8>(~0b1001011) << std::endl; }
affiche :
~00100100 = 11011011 ~01001011 = 10110100
Si vous n'utilisez pas std::bitset, mais affichez en héxadécimal, le résultat est un peu différent :
- main.cpp
#include <iostream> int main() { std::cout << std::showbase << std::hex; std::cout << 0b1 << std::endl; std::cout << ~0b1 << std::endl; std::cout << std::endl; std::cout << 0b0110011 << std::endl; std::cout << ~0b0110011 << std::endl; }
affiche :
0x1 0xfffffffe 0x33 0xffffffcc
Le résultat peut paraître surprenant. Si on réécrit ces deux nombres en binaire et qu'on les aligne avec les valeurs binaires d'origine, on obtient :
0b1 = 1 0xfffffffe = 1111 1111 1111 1111 1111 1111 1111 1110 0b110011 = 11 0011 0xffffffcc = 1111 1111 1111 1111 1111 1111 1100 1100
ajouter un schéma, comme pour les opérateurs suivants
Si on se rappelle que les 0 devant un nombre peuvent être ignorés (1 = 01 = 001 = 0001, etc.), on comprend que l'opération est réalisée sur des nombres entiers de 32 bits (ou 4 octets), quelque soit le nombre de bits que l'on utilise pour écrire le nombre. Les 0 manquants devant le nombre sont ajoutés avant l'opération.
Cela signifie qu'en interne, ces nombres entiers sont représentés par défaut sur 32 bits (4 octets), quelque soit le nombre de bits utilisés pour les écrire.
Le décalage de bits
Un autre type d'opérateur logique sont les opérations de décalage à droite » et à gauche «. Ces opération permettent de décaler les bits à droite ou à gauche d'un certain nombre de bits. Par exemple :
- main.cpp
#include <iostream> int main() { std::cout << std::hex << std::showbase; std::cout << (0b11011000 << 1) << std::endl; // décalage de 1 bit à gauche std::cout << (0b11011000 << 2) << std::endl; // décalage de 2 bit à gauche std::cout << std::endl; std::cout << (0b11011000 >> 1) << std::endl; // décalage de 1 bit à droite std::cout << (0b11011000 >> 2) << std::endl; // décalage de 2 bit à droite }
« et » et les opérateurs de flux « et », ce qui ne produira pas le comportement attendu.
Plus généralement, il faudra faire attention en C++ à la syntaxe, un même opérateur pouvant signifier des choses différentes selon le contexte.
affiche :
0x1b0 0x360 0x6c 0x36
Affichons les valeurs en binaire et alignons les pour mieux comprendre :
0b11011000 = 0000 0000 0000 0000 0000 0000 1101 1000 0x1b0 = 0000 0000 0000 0000 0000 0001 1011 0000 // décalage de 1 bit à gauche 0x360 = 0000 0000 0000 0000 0000 0011 0110 0000 // décalage de 2 bit à gauche 0x6c = 0000 0000 0000 0000 0000 0000 0110 1100 // décalage de 1 bit à droite 0x36 = 0000 0000 0000 0000 0000 0000 0011 0110 // décalage de 2 bit à droite
Prenons par exemple le premier décalage (décalage de 1 bit à gauche). Avec un schéma, cela devrait être encore plus clair :
On voit :
- que la séquence de 0 et de 1 est identique ;
- qu'elle est décalée de 1 bit vers la gauche ;
- qu'un 0 est inséré à droite ;
- que le 0 à gauche est perdu.
Exos : comparer les division et multiplication par 2, 4, etc avec les décalage
Les opérateurs logiques bit à bit
Pour terminer, il existe les opérateurs logiques “AND” (“ET”) &, “OR” (“OU”) | et XOR (“OU Exclusif”) ^ pour les nombres. Ils sont similaires aux opérateurs de même nom que vous avez vu précédemment pour les booléens, sauf qu'ils s'appliquent sur chaque bit d'un nombre. Ainsi, le premier bit du résultat est calculé à partir du premier bit de chaque nombre, le deuxième bit du résultat à partir du deuxième bit de chaque nombre, et ainsi de suite. L'opérateur “OU exclusif” n'a pas d'équivalent pour les booléens, pour rappel il retourne vrai lorsque l'une des opérandes est vraie, mais pas les deux.
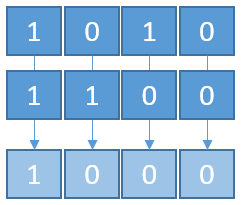
Par exemple, pour l'opérateur “AND”, on aura le schéma suivant :
Le code suivant permet de vérifier les différents opérateurs logique :
- main.cpp
#include <iostream> #include <bitset> int main() { std::cout << " " << std::bitset<8>(0b1010) << std::endl; std::cout << " " << std::bitset<8>(0b1100) << std::endl; std::cout << " --------" << std::endl; std::cout << "& " << std::bitset<8>(0b1010 & 0b1100) << std::endl; // AND std::cout << "| " << std::bitset<8>(0b1010 | 0b1100) << std::endl; // OR std::cout << "^ " << std::bitset<8>(0b1010 ^ 0b1100) << std::endl; // XOR }
affiche :
00001010 00001100 -------- & 00001000 | 00001110 ^ 00000110
On retrouve les tables logiques données pour les booléens :
a | b | ~a | a & b | a | b | a ^ b |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |