Outils d'utilisateurs
Ceci est une ancienne révision du document !
Table des matières
| Chapitre précédent | Sommaire principal | Chapitre suivant |
|---|
Logique binaire et calcul booléen
Comme vous l'avez vu au chapitre précédent, vous pouvez écrire les nombres en base 2, encore appelé binaire, en utilisant la syntaxe 0b. Les nombres binaires ont un intérêt particulier dans le monde de l'informatique. Les ordinateurs fonctionnent à la base avec des signaux électriques, il est très facile de représenter une valeur pouvant prendre deux états en électronique. Par exemple, on peut dire qu'un tension basse (autour de 0 volts) représente un état et une tension haute (autour de 5 volts) à un autre état.
Il est possible de nommer ces deux états de différentes manières, selon le contexte ou les habitudes. On peut par exemple parler d'états “haut” et “bas”, “oui” et “non”, “vrai” ou “faux”, “0” ou “1”, etc. En C++, vous avez deux manière de représenter une valeur binaire :
- pour écrire un nombre entier en utilisant le mode binaire avec
0bet des 0 et 1 ; - pour écrire une valeur binaire, en utilisant les mots-clés
true(vrai) etfalse(faux).
Les booléens
Voyons dans un premier temps les valeurs binaires, encore appelées booléens (nom donné en l'honneur du mathématicien George Boole, qui a créé cette branche des mathématiques).
Pour écrire une valeur booléenne, il faut utiliser les mots-clé true (vrai) et false (faux). Par défaut, cout affiche ces valeurs avec respectivement 1 et 0. La directive std::boolalpha permet d'afficher les booléens en clair.
- main.cpp
#include <iostream> int main() { std::cout << "false = " << false << std::endl; std::cout << "true = " << true << std::endl; std::cout << std::boolalpha; std::cout << "false = " << false << std::endl; std::cout << "true = " << true << std::endl; }
affiche :
false = 0 true = 1 false = false true = true
Les opérateurs logiques
Les booléens ne se manipulent pas comme des nombres entiers et cela n'a pas de sens de faire des opérations arithmétiques dessus. Les booléens permettent un nombre limité d'opérations, qui prennent un ou deux booléens et retourne un nouveau booléen.
true+2. Il faut comprendre que le C++ est un langage permissif, qui fait confiance aux développeurs par défaut.
C'est donc à vous d'écrire du code en suivant certaines règles de codage et en respectant les sémantiques. Et donc, même si true+2 est autorisé par la norme du langage, cela n'a pas de sens en termes de sémantique (si on vous demande “est-ce qu'il faut beau aujourd'hui ?”, cela n'a pas de sens de réponse “oui plus deux”).
La première opération booléenne est la négation “NON” !, qui transforme true en false et false en true :
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "!false = " << !false << std::endl; std::cout << "!true = " << !true << std::endl; }
affiche :
!false = true !true = false
La seconde opération est la conjonction &&, qui prend deux booléens et retourne vrai uniquement si les deux booléens sont vrai. Cette opération est également appelée “AND” ou “ET”, puisque pour que le résultat soit vrai, il faut que le premier booléen soit vrai ET que le second booléen soit vrai.
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "false AND false = " << (false && false) << std::endl; std::cout << "false AND true = " << (false && true) << std::endl; std::cout << "true AND false = " << (true && false) << std::endl; std::cout << "true AND true = " << (true && true) << std::endl; }
affiche :
false AND false = false false AND true = false true AND false = false true AND true = true
La dernière opérateur est la disjonction ||, qui prend également deux booléens et retourne vrai si au moins un des deux booléens est vrai. Cette opération est également appelée “OR” ou “OU”, puisque pour que le résultat soit vrai, il faut que le premier booléen soit vrai OU que le second booléen soit vrai.
- main.cpp
#include <iostream> int main() { std::cout << std::boolalpha; std::cout << "false OR false = " << (false || false) << std::endl; std::cout << "false OR true = " << (false || true) << std::endl; std::cout << "true OR false = " << (true || false) << std::endl; std::cout << "true OR true = " << (true || true) << std::endl; }
affiche :
false OR false = false false OR true = true true OR false = true true OR true = true
Ces opérateurs peuvent être résumé dans un tableau :
a | b | !a | a && b | a || b |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
Un point important pour terminer. Les opérateurs logiques du C++ fonctionne en utilisant l'évaluation paresseuse (lazy evaluation). Cela permet d'évaluer les opérandes uniquement si nécessaire. Imaginons les tests suivant :
a && (expression compliquée) a || (expression compliquée)
dans lesquelles “opération compliquée” est un code quelconque qui prend du temps a être évaluer. Avec le tableau précédent, on peut remarquer un point : si “a” est faux, alors que le résultat de “a && b” sera toujours faux, quelque soit la valeur de “b”. Dans ce cas, il n'est pas nécessaire d'évaluer “b”, puisque sa valeur ne change par le résultat. Donc dans l'expression suivante :
a && (expression compliquée)
Si “a” est faux, “expression compliquée” n'est pas évaluée et le résultat retournée sera faux. “Expression compliquée” ne sera évaluer que si “a” est vrai.
De la même façon, si “a” est vrai dans la seconde expression avec “OR”, le résultat sera toujours vrai et il n'est pas nécessaire d'évaluer “expression complexe”. “Expression compliquée” ne sera évaluer que si “a” est faux.
a || (expression compliquée)
Les opérateurs de comparaison
L'algèbre de bool
La représentation binaire
Voyons maintenant la représentation binaire des nombres entiers. Vous avez vu dans le chapitre précédent comment écrire un nombre selon cette représentation. Dans la représentation binaire, chaque chiffre 0 ou 1 est appelé un bit. Lorsque vous affichez ce nombre, la valeur est affichée (par défaut) selon la base 10 (décimale).
- main.cpp
#include <iostream> int main() { std::cout << 0b101010 << std::endl; }
affiche :
42
Il n'existe pas de directive pour afficher les nombres directement en binaire, on utilise souvent à la place le représentation hexadécimale. La raison est qu'il est relativement facile de faire la conversion entre hexadécimale et le binaire. En effet, un chiffre hexadécimal correspond exactement à quatre chiffres binaires, il faut donc utiliser la conversion suivante :
| hexadécimal | binaire | hexadécimal | binaire |
|---|---|---|---|
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | a | 1010 |
| 3 | 0011 | b | 1011 |
| 4 | 0100 | c | 1100 |
| 5 | 0101 | d | 1101 |
| 6 | 0110 | e | 1110 |
| 7 | 0111 | f | 1111 |
Ainsi, pour convertir la valeur 0x42 en binaire, vous devez prendre le premier chiffre (4), le convertir en binaire (0100), puis faire la même chose avec le second chiffre (2, ce qui donne 0010). La représentation binaire finale est donc 0b01000010.
Une séquence de 8 bits (ou de 2 chiffres hexadécimaux, cela revient au même) est appelée un octet (1 o), 1024 octets donnent 1 kilo octet (1 ko), 1024 ko donnent 1 méga octets (1 Mo), 1024 méga octets donnent 1 giga octets (1 Go), 1024 giga octets donnent 1 tera octets (1 To).
Les opérateurs arithmétiques
Maintenant que vous savez écrire et lire les nombres binaires, vous allez pouvoir les manipuler. Comme ce sont des nombres entiers, les opérateurs arithmétiques présentés dans le chapitre précédent peuvent être utilisé :
- main.cpp
#include <iostream> int main() { std::cout << 0b1010 + 0b1011 << std::endl; // addition std::cout << 0b0011 - 0b1101 << std::endl; // soustraction std::cout << 0b1000 * 0b1011 << std::endl; // multiplication std::cout << 0b1001 / 0b0010 << std::endl; // division entière }
affiche :
21 -10 88 4
L'opérateur négation
En complément de ces opérateurs arithmétiques, il existe des opérateurs travaillant sur la représentation binaire, que l'on appelle opérateurs logiques bit à bit. Le premier opérateur est la négation ~, qui permet d'inverser tous les bits d'un nombre (les 0 deviennent de 1 et les 1 deviennent des 0). Par exemple :
- main.cpp
#include <iostream> int main() { std::cout << std::hex << std::showbase; std::cout << ~0b1 << std::endl; std::cout << ~0b110011 << std::endl; }
affiche :
0xfffffffe 0xffffffcc
Le résultat peut paraître surprenant. Si on réécrit ces deux nombres en binaire et qu'on les aligne avec les valeurs binaires d'origine, on obtient :
0b1 = 1 0xfffffffe = 1111 1111 1111 1111 1111 1111 1111 1110 0b110011 = 11 0011 0xffffffcc = 1111 1111 1111 1111 1111 1111 1100 1100
Si on se rappelle que les 0 devant un nombre peuvent être ignorés (1 = 01 = 001 = 0001, etc.), on comprend que l'opération est réalisée sur des nombres entiers de 32 bits (ou 4 octets), quelque soit le nombre de bits que l'on utilise pour écrire le nombre. Les 0 manquant devant le nombre sont ajoutés avant l'opération.
Un autre type d'opérateur logique sont les opérations de décalage à droite » et à gauche «. Ces opération permettent de décaler les bits à droite ou à gauche d'un certain nombre de bits. Par exemple :
- main.cpp
#include <iostream> int main() { std::cout << std::hex << std::showbase; std::cout << (0b11011000 << 1) << std::endl; // décalage de 1 bit à gauche std::cout << (0b11011000 << 2) << std::endl; // décalage de 2 bit à gauche std::cout << (0b11011000 >> 1) << std::endl; // décalage de 1 bit à droite std::cout << (0b11011000 >> 2) << std::endl; // décalage de 2 bit à droite }
« et » et les opérateurs de flux « et », ce qui ne produira pas le comportement attendu.
Plus généralement, il faudra faire attention en C++ à la syntaxe, un même opérateur pouvant signifiant des choses différentes selon le contexte.
affiche :
0x1b0 0x360 0x6c 0x36
Affichons les valeurs en binaire et alignons les pour mieux comprendre :
0b11011000 = 0000 0000 0000 0000 0000 0000 1101 1000 0x1b0 = 0000 0000 0000 0000 0000 0001 1011 0000 // décalage de 1 bit à gauche 0x360 = 0000 0000 0000 0000 0000 0011 0110 0000 // décalage de 2 bit à gauche 0x6c = 0000 0000 0000 0000 0000 0000 0110 1100 // décalage de 1 bit à droite 0x36 = 0000 0000 0000 0000 0000 0000 0011 0110 // décalage de 2 bit à droite
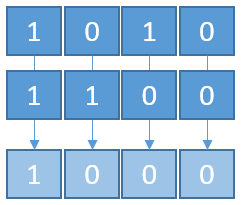
Prenons par exemple le premier décalage (décalage de 1 bit à gauche). Avec un schéma, cela devrait être encore plus clair :
On voit :
- que la séquence de 0 et de 1 est identique ;
- qu'elle est décalée de 1 bit vers la gauche ;
- qu'un 0 est inséré à droite ;
- que le 0 à gauche est perdu.
division et multiplication par 2, 4, etc avec les décalage
Les opérateurs logiques bit à bit
Pour terminer, il existe les opérateurs logique “AND” (“ET”) &, “OR” (“OR”) | et XOR (“OU Exclusif”) ^ pour les nombres. Ils sont similaire aux opérateurs de même nom que vous avez vu précédemment pour les booléens, sauf qu'ils s'appliquent sur chaque bit d'un nombre. Ainsi, le premier bit du résultat est calculé à partir du premier bit de chaque nombre, le deuxième bit du résultat à partir du deuxième bit de chaque nombre, et ainsi de suite. L'opération “OU exclusif” n'a pas d'équivalent avec les booléens, il correspond à vrai lorsque une seule de valeur est vrai, pas les deux.
Le code suivant permet de vérifier les différents opérateurs logique :
- main.cpp
#include <iostream> int main() { std::cout << std::hex << std::showbase; std::cout << (0b1010 & 0b1100) << std::endl; // AND std::cout << (0b1010 | 0b1100) << std::endl; // OR std::cout << (0b1010 ^ 0b1100) << std::endl; // XOR }
affiche :
0x8 0xe 0x6
Si on convertie en binaire, on obtient :
0b1010 = 1 0 1 0 0b1100 = 1 1 0 0 0x8 = 1 0 0 0 // AND 0xe = 1 1 1 0 // OR 0x6 = 0 1 1 0 // XOR
On retrouve les tables logiques données pour les booléens :
a | b | ~a | a & b | a | b | a ^ b |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
utilisation de mask avec opérateur logiques
Exercices
Algèbre de Bool
Il est possible d'écrire des opérations logiques complexes, à 2 ou plus arguments, avec les opérateurs de base NON, ET, OU et OU EXCLUSIF.
- Ecrire les séries suivantes : ???
- En particulier, NON-ET permet de réécrire tous les autres opérateurs. Le faire.
Les opérateurs arithmétiques
Dans un ordinateur, composé de transistors, forment des portes logiques. Ces portes permet de réaliser tous les calculs.
- pour 1 bit, réécrire l'addition avec les opération logiques
- uniquement avec NAND
- pour 8 bits, idem
| Chapitre précédent | Sommaire principal | Chapitre suivant |
|---|