Les nombres réels sont intéressants, puisqu'ils permettent de représenter des nombres plus grands que les nombres entiers. Si par exemple, vous essayez d’exécuter le code suivant :

main.cpp

#include <iostream>
 
int main() {
    std::cout << 9223372036854775808 << std::endl;
}

vous obtiendrez une erreur (seules les premières erreurs sont copiées ici) :

main.cpp:4:26: warning: integer constant is so large that it is unsigned
     std::cout << "  " << 9223372036854775808 << std::endl;
                          ^
main.cpp: In function 'int main()':
main.cpp:4:15: error: ambiguous overload for 'operator<<' (operand types are 
'std::basic_ostream<char>' and '__int128')
     std::cout << 9223372036854775808 << std::endl;
               ^
...

La première erreur “integer constant is so large that it is unsigned” indique que le nombre entré est tellement grand qu'il n'existe pas de type signé (signed, qui peut représenter de nombres positifs et négatifs) qui peut représenter ce nombre. Le compilateur est donc obligé d'utiliser un type non signé (unsigned, qui ne peut représenter que des nombres positifs).

La seconde erreur “ambiguous overload” indique que le compilateur ne sait pas comment afficher ce nombre (plus précisément, il ne sait pas quel opérateur « utiliser avec std::cout pour afficher ce nombre).

Note : ce nombre n'a pas été choisit au hasard. Il s'agit du plus grand nombre représentable avec les types de base du C++, plus un. Vous verrez par la suite comment obtenir des informations sur les types, comme par exemple la valeur maximale possible.

Si on modifie un tout petit peu ce code (en ajoutant une décimale), pour utiliser un nombre réel, le compilateur ne produit plus d'erreur :

main.cpp

#include <iostream>
 
int main() {
    std::cout << 9223372036854775808.0 << std::endl;
}

affiche :

9.22337e+18

Comme on peut s'y attendre, le programme affiche le nombre en utilisant la notation scientifique.

Pour autant, les nombres réels ne sont pas parfaits non plus (sinon, on ne s’embêterait pas à faire la distinction entre entiers et réels). Prenons un autre code d'exemple :

main.cpp

#include <iostream>
 
int main() {
    std::cout << "  " << (9223372036854775807 - 9223372036854775806) << std::endl;
    std::cout << "  " << (9223372036854775807.0 - 9223372036854775806.0) << std::endl;
}

affiche :

1
0

On a donc deux nombres, représentées dans le premier cas par des entiers et dans le second par des réels (notez la décimale). Ces deux nombres sont grands, mais peuvent être représentés sans problème par des entiers en C++ (plus précisément par le type long long int, que vous verrez ensuite). La différence entre ces deux nombres vaut un.

Dans tous les cas, les nombres en C++ sont représentés par un nombre fini d'octets dans la mémoire des ordinateurs. Il n'est donc pas possible de représenter tous les nombres possibles (ce qui n'aurait de toute façon aucun sens, puisque qu'il existe une infinité de nombres réels). Les nombres réels peuvent représenter des nombres plus grands que les nombres entiers parce qu'ils ne peuvent pas représenter les grands nombres avec la même précision que les nombres entiers.

Dans le code d'exemple précédent, les nombres entiers ne sont pas arrondis et le calcul est juste. Au contraire, les nombres réels sont arrondis et sont représentées par la même valeur en mémoire. Le calcul se fait donc sur la même valeur et le résultat est nul.

Imaginons que vous souhaitez travailler sur des nombres décimaux, mais en conservant la précision des nombres entiers (vous ne voulez pas que les valeurs soient arrondies). Par exemple, dans une application bancaire, qui manipule des centimes (deux chiffres après la virgule).

Le principe des nombres à virgule fixe est relativement simple : au lieu de manipuler des nombres réels, on va multiplier les valeurs par un facteur constant (généralement un multiple de 10) et utiliser cette représentation pour faire les calculs. C'est uniquement lors de l'affichage que l'on va recalculer la valeur décimale exacte.

Par exemple, dans le cas d'une application bancaire, on peut utiliser un facteur 100 :

  1    =   100
 12.34 =  1234
123.4  = 12340

En C++, il est possible de créer un nouveau type de nombre, qui permet de représenter plus facilement des nombres à virgule fixe, mais vous verrez cela dans la partie sur la programmation objet. Dans ce chapitre, nous allons simplement utiliser un facteur directement dans le code. Ce n'est pas l’idéal en termes de conception, mais c'est suffisant pour le moment pour étudier le fonctionnement de cette représentation.

Définir une représentation n'est pas suffisante, il faut également définir les opérations arithmétiques de base. Pour l'addition et la soustraction, les opérateurs par défaut des entiers fonctionnent sans problème.

1.2 + 3.4 = 4.6
120 + 340 = 460 // facteur 100

Pour la multiplication et la division, il faut faire une correction : il faut diviser le résultat par le facteur pour la multiplication et multiplier par le facteur pour la division. Par exemple, pour la multiplication :

#include <iostream>

int main() {
    std::cout << (1.2 * 3.4) << std::endl;
    std::cout << (120 * 340) / 100 << std::endl;
}

affiche :

4.08
408

Remarque : pour la division, le résultat en utilisant des nombres réels peut avoir plus de chiffres après la virgule que les opérandes. En utilisant les nombres à virgule fixe, ces décimales supplémentaires seront perdues. Encore une fois, on doit faire un compromis avec la précision. Si cet arrondi est problématique, il faudra utiliser un facteur plus important ou utiliser des nombres réels.

Exercice : démontrer mathématiquement les propriétés précédentes pour la multiplication et la division.

Supposons que vous souhaitez compter de 0 à 10 avec un pas de un tiers (cela signifie que vous incrémentez votre compteur de 1/3 à chaque fois). Pour cela, vous allez écrire un code similaire au code suivant (en pseudo-code, pas en C++) :

compteur = compteur + 1.0 / 3.0;
utiliser(compteur);

Remarque : un identifiant comme compteur, qui permet de se souvenir d'une valeur, est appelée une variable. Vous verrez cela dans les prochains cours.

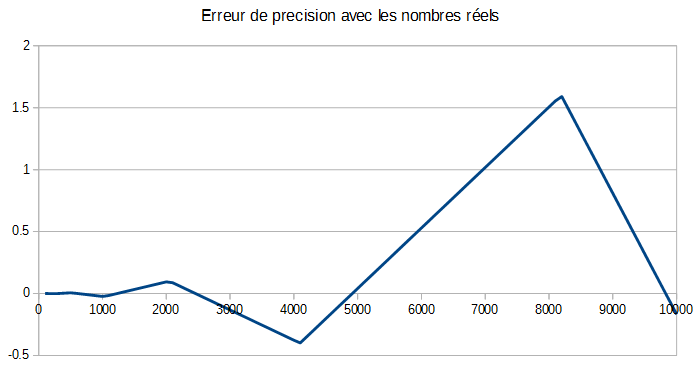
Si vous répétez ce calcul, la différence entre la valeur calculée et la valeur correcte attendue va progressivement augmenter. Le graphique suivant représente l'erreur de calcul en fonction de la valeur du compteur :

Note : pour mieux voir le phénomène, j'ai volontairement utilisé des nombres réels sur 32 bits (simple précision). Il existe des types de nombres réels plus précis, mais ce n'est pas important ici. Le problème existe avec tous les types de nombres réels, la seule différence est qu'il met plus de temps à apparaître.

Vous voyez que l'erreur devient assez vite importante. Selon vos besoins, vous pouvez accepter les valeurs en dessous de 1000, mais l'erreur devient trop importante au-delà.

La solution est assez simple (vous l'aurez deviné, vu que l'on est dans le chapitre sur les nombres à virgule fixe) : il suffit d'utiliser un compteur entier, qui sera incrémenté de 1 à chaque fois. La valeur du compteur réel sera obtenue en divisant par 3.

compteur = compteur + 1;
utiliser(compteur / 3.0);

Avec un compteur réel, si on compte jusqu'à 10 000, il y aura 30 000 additions réelles, chaque addition ajoutant une erreur (presque infime) de calcul. Ces erreurs vont s'accumuler, jusqu'au point de ne plus être négligeables.

Avec le compteur entier, comme chaque addition est exacte, les 30 000 additions ne produisent pas d'erreur de calcul. La seule opération réalisée sur des nombres réels (donc avec une erreur de précision) est la division par 3. L'erreur de calcul finale est donc l'erreur sur une seule opération réelle, ce qui reste négligeable.

Voir l'article sur Wikipedia : Fixed-point arithmetic.